Kazunori OTSUKA*,Tomizou OKUDA 大塚　一徳*奥田　富蔵 Analysis of strategies for Mastermind −analysis by protocol data − Mastermindにおけるプレーヤーの解決方略 −発話プロトコルによる解決過程の分析− Abstract 　In the current study, we proposed the model of problem solving process for Mastermind, which is a number guessing game, to investigate problem solving process and problem solving strategy. And we semantically analyzed the protocol data of 4 subjects(from 18 years old to 26 years old) who played the three-dimensional versions of Mastermind. Results revealed the subjects used different strategy each other, and used adaptable strategy as game situation. Key words：working memory, problem solving, reading span test, mastermind

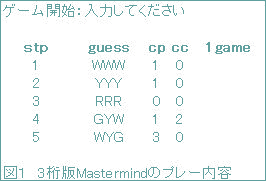
1. 目的 1.1 Mastermind 　本研究は，固有の知識領域に依存しない簡易なゲームで，数当てゲームの一種であるMastermind1)というゲームの解決過程を，被験者の利用方略の点から探索的に分析し検討することを目的とするものである。 　領域固有の知識に依存しないゲームなどを課題とした問題解決事態の研究では，従来解決のための手がかりが事前に明示されている課題を取り扱ったものが多かった。一方，本研究でとりあげるMastermindは，解決のための手がかりがあらかじめ明示されておらず，継時的に集積する情報の中に解決の手がかりが存在するという特性を持っている２）。 　Mastermindは，パソコン上でランダムに生成される秘密の色の組み合わせを,プレーヤーができるだけ少ない質問回数で当てることを競うゲームである。本研究では，緑（G），赤（R），黄（Y），白（W）の4色から3個の色を並べる重複順列で64個の正解コードが存在するパターン（3桁版Mastermind）を利用する。図1は3桁版Mastermindのプレー内容を図示したものである。 　本研究では，プレーヤーが選択する色の組み合わせのことを質問コードと呼び，当てるべき色の組み合わせを正解コードと呼ぶことにする。cp（Correct Position）値，cc（Correct Color）値は質問コードに対するフィードバック情報で，cp値はある試行において位置も色も一致するものの個数であり，cc値はcp値で対象となったコード以外で位置は異なるが色は一致するものの個数である。図1のように3桁版Mastermindでは，cp値・cc値がそれぞれ3，0になって終了する。図1の場合，正解コードはWYGである。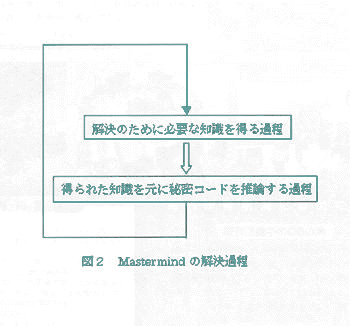 　この実験課題は，解決の際に特別の前提知識を必要とせず，人間一般が持つ量や順序などに関する基本的な知識とゲームのルールから解を導き出せる課題である3)。また，ハノイの塔問題4)や放射線問題5)などのように，これまでの問題解決の研究で多く使われてきた問題が解決のための手掛かり情報が予め付与されているのに対して，Mastermindの問題解決事態では解決のための手掛かり情報が予め付与されず解決過程で徐々に呈示され，しかもその手掛かり情報は一時的なものでゲームごとに異なるという特徴がある3)。 　1.2 Mastermindの解決過程と解決方略 　図2に示すように，Mastermindの解決過程は大きく2段階に別れる。”解決のために必要な知識を得る過程”においては，プレーヤーは解決に必要な知識すなわち解決のための手掛かり情報を得なければならない。 　Mastermindにおける手掛かり情報とは，１ゲーム内における各試行ごとの質問コードとそれに対応したcp値，cc値すなわち評価値をもとに導かれる解決のために有用となる情報のことである。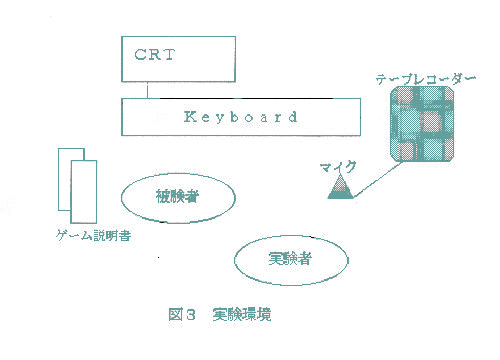 　次に，”得られた知識をもとに秘密コードを推論する過程”において，プレーヤーはそのゲームにおいて獲得した手掛かり情報をもとに正解コードを推論する。正解コードの推論が不成功に終わった場合は，再度この2つの過程を繰り返すこととなる。 　よく定義された問題としてのゲームの解決方略に関しては，これまで認知心理学的に多くの分析が試みられている。例えば，ハノイの塔問題が解決の手掛かりが予め付与される情報の中にある自己完結的事態と考えられるのに対して，Mastermindは，継時的に集積していく情報の中に解決の手掛かりがあり，課題状況に応じて柔軟に対処する事が必要となってくる6)。 　領域固有の知識に依存しないゲームなどを課題とした問題解決事態の研究では、従来解決のための手掛かりが事前に明示されている課題を取り扱ったものが多かった。一方，本研究でとりあげるMastermindは解決のための手がかりがあらかじめ明示されておらず。継時的に集積する情報の中に解決の手がかりが存在するという特性を持っている。様々な状況に適応し，柔軟に対処する人間の思考過程の解明のためには，状況適応的な対処が必要とされるMastermind のような 課題 における 発見法的解決方略（heuristic）の分析が必要であると思われる。 　そのためには，Mastermindにおいてプレーヤーが実際にどのような解決方略を利用しているのか，またそれは課題の状況とプレー知識の集積によってどのように異なるかといった点について詳細な分析が必要である。本研究ではこのような観点から，Mastermindにおける発見法的解決方略の考察と実験的分析を試みることを目的とする。 　Mastermindあるいは同様の課題に関するこれまでの心理学的研究では、このような応答的問題解決事態で用いられる解決方略についても報告されている。 　Bruner,Goodnow, & Austin7)は，概念学習実験において数当てゲームと同様の選択事態における結合概念の獲得において選択事例のパターンから焦点方略と走査方略を報告している。また，Bruner et al.らの研究を基にLaughlin,Lange, & Adamopoulos8）は，Mastermindにおいて焦点方略と戦略的方略について分析している。米川6)は，数当てゲームにおいて直前の情報を基に推論を進める部分確定型の方略と集積した情報の整合性をとりながら推論を進める情報集約型の方略の二つの方略を報告している。 　本研究で検討されるMastermindと同じ３桁４色の課題に関して奥田ら3)は，効率的な解決方略として数え挙げによる方略と演繹的推論による方略について分析し，前者は短期記憶の容量に制限がある人間には適当ではないこと，後者に関しては領域知識に強く依存し，かなり習熟した後でないと可能ではないと指摘している。 　以上のような先行研究の結果を踏まえ，本研究ではMastermindにおいて利用される発見法的解決方略のモデルを提示し，実験的に行ったゲームにおけるプロトコルをその方略モデルを基に意味的に分析し，それを基に本ゲームにおいてプレーヤーが用いる発見法的解決方略について考察を加える。 　Bruner et al.らの選択事態とは異なりMaster- mindにおいては，位置と色に関するフィードバック情報という多義性のあるフィードバック情報からプレーヤーは発見法的な方略をプレーの状況に応じて使いわけているということが予測される。また，Mastermindにおける問題解決は，位置という次元とその位置の色という属性に関する知識を獲得する過程であると考えられる。従って，先行研究を基にMastermindの解決方略を位置と色に関する知識を獲得するための方略と考え，以下のような解決方略のモデルを設定した。 （１）試行錯誤方略（Trial and Error strategy:以下 ＴＥと略す） 　 全くランダムな色の組み合わせを質問し，試行錯誤的に情報を得ようとする方略。 （２）位置に関する焦点方略（Focusing Correct Position:以下ＦＣＰと略す） cp値から特定の位置の秘密コードを同定するための質問コードを選択していく方略。 （３）色に関する焦点方略（Focusing Correct Color:以下ＦＣＣと略す） 位置には関係なく秘密コードに含まれる色とその個数に関するプレー知識を得るための質問コードを選択する方略。 （４）位置に関する走査方略（Scanning Correct Position:以下ＳＣＰと略す） cp値に関する仮説を立てその仮説をもとに質問コード決め仮説を検証していく方略。 （５）色に関する走査方略（Scanning Correct color:以下ＳＣＣと略す） cc値に関する仮説を立てその仮説をもとに質問コード決め仮説を検証していく方略。 （６）プレー知識による推論方略（Knowledge Based Inference:以下ＫＢＩと略す） 集積したプレー知識と質問コードをもとに秘密コードを推論する方略。 （１）から（５）はプレー知識（手掛かり情報）を得るためにどのような質問コードを選択するかについての方略であり，図２の”解決のために必要な知識を得る過程”において用いられる。（６）は得られたプレー知識と質問コード，フィードバック情報からゲームの制約条件を考慮しながら推論を進めていく過程であり，図２の”得られた知識をもとに秘密コードを推論する過程”において用いられる方略と考えられる。 2. 方法 2.1　実験課題 　３桁版Mastermind。ゲームは本実験用にパソコン上で利用するゲームとして作成されたもので，自動的に各被験者の各試行ごとの反応時間，質問コード，試行回数，各ゲームごとの正解コードが履歴ファイル上に保存された。被験者はパソコン上でゲームを行っていき，例えばGRYとキーボードから入力しリターンキーを押すという試行を正解コードを見つけるまで繰り返して行った。実験中被験者は，メモや筆記具を利用することはできなかった。正解コードはランダムに選ばれ，1ゲーム中被験者は10試行まで可能であった。 2.2 被験者及び手続き 　被験者は18歳から26歳までの４名の成人であった。全ての被験者はパソコンの操作に関しては6ヶ月以上の経験があった。また，過去にこのゲームを行った経験のある被験者はいなかった。 実験は図3に示される環境で行われた。 　被験者は，本実験でのMastermindのルール，キーボードの操作等についての説明書を読んだ後，予備試行として２ゲームないしは３ゲームを行った。その後本実験に入り，５ゲームないしは６ゲームを被験者は行った。ゲームの説明では”できるだけ少ない回数で正解コードを見つける”というゲームの主旨が強調された。実験中，主に発問法により被験者の発話プロトコルを収集した。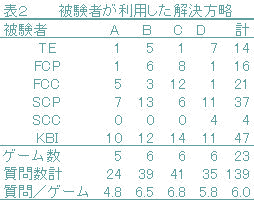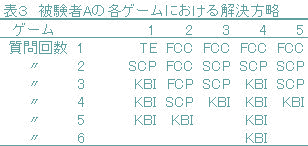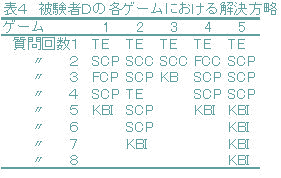 3. 結果 　実験で被験者は合計139個の質問コードを生成していた。そこで実験後，139個の中の各々の質問コードごとにプロトコルとその前後のcp値，cc値及び前後の質問コードの意味的な分析を行った。本研究で行った意味的な分析においては前述の解決方略モデルに基づき, YYY，WWWといった3桁とも同一の色の質問はＦＣＣ方略として分類した。また，cp値にのみフィードバック情報があり，その情報を基に次の質問コードを仮定していることがあきらかな場合ＦＣＰ方略として分類した（表１，ＦＣＰ方略参照）。また，ＳＣＰ・ＳＣＣ方略に関しては主にプロトコル内容により分析した。さらに，ＴＥ方略は主に第１試行目の質問コードに適用し，ＫＢＩ方略は１ゲームの後半における質問コードとプロトコルによって判断した。表1は被験者の発話プロトコルの例を示したものである。表1に例示されるような意味的な分析をもとに，被験者の質問コードを上記の６つの解決方略モデルに基づいて分類した結果が表2である。また被験者Ａがゲームごとに使用した方略をまとめたものが表3であり，被験者Ｄがゲームごとに使用した方略をまとめたものが表4である。 4. 考察 　本研究では実験における被験者の発話プロトコルをMastermindにおいて利用される発見法的解決方略のモデルを基に意味的に分析し，それを基に本ゲームにおいてプレーヤーが用いる発見法的解決方略について考察を加えることが目的であった。 　表2においてプレーヤーによって利用される方略が異なる事が示されており，一時的に記憶している手掛かり情報や，その時点の質問コードとフィードバック情報といった課題の状況に応じて，被験者が方略を使い分けていることが示されたといえる。また表3においては後半にＫＢＩ方略が多く利用されていることが示されている。表３，表４に示されるように（１）から（５）までの方略は，手掛かり情報となるプレー知識を得るために質問コードを選択する際の方略であり，ゲームの前半で主に用いられる方略であることが示唆される。一方，ゲームの後半では質問コードとフィードバック情報及びプレー知識から制約条件を充足するように秘密コードを推論する過程であり，特定のプレー知識を基に帰納的に推論を進めているのではないかと考えられる。 　さらに表2から，利用される解決方略の頻度は被験者によってかなり個人差が見られることも示されている。この点について被験者Ａのプレー内容をまとめた表3を検討してみると以下のような解決過程に関する分析が可能である。すなわち，被験者Ａは”まず色に関する情報を集め，それを基に仮説検証を行い獲得したプレー知識を基に推論を進める”という解決過程である。被験者Ａが，プレー全体を見通したうえで1試行目から方略の適応を考えていたことが推測される。また，被験者Ａのように第1試行目から色に焦点をあてたＦＣＣ方略を用いるといった解決過程は，被験者Ｂ・Ｃにも同様に観察された。ＦＣＣは，もっとも被験者に対する認知的負荷が少ない方略であり9)，被験者が認知的負荷を軽減する方略を頻繁に利用することが示唆されたといえる。 　 一方，被験者Ｄは，第1試行目の結果によって第2試行目以降の方略を変化させゲーム状況に対応させているような解決過程を辿っていることが，表4から推測される。被験者Ｄにおいては，プレー全体を見通したプランの構成能力や，課題状況に応じた方略の適用能力がMastermindの解決過程において重要な役割を果たすことが示唆されたといえる。 　Mastermindの解決過程に影響を及ぼす認知的要因の1つとして大塚・奥田10)は作動記憶（Working Memory）の処理資源に焦点をあて検討を行い，作動記憶容量の個人差がMastermindのような問題解決過程に影響を及ぼす重要な認知的要因の1つであることを示している。例えば，獲得したプレー知識によって推論を進めていく場合でも必ずしも正しい推論を行っていない場合も観察された。このような誤判断は，制約条件によるものか，被験者の作動記憶容量の個人差や推論能力の欠如によるものかといった点について，今後詳細な検討が必要である。 　今回の実験では，ＳＣＣ方略はあまり見られなかった。Laugln et al8)らの研究と同様に被験者の利用した方略から判断すると，ＦＣＣ，ＳＣＣという色に関する焦点方略と，位置に関する仮説検証的な走査方略という2つの方略をMastermindの解決方略として想定できると思われる。 　Mastermindはゲームとして適度の複雑さをもち，またコンピュータ化することでゲーム過程を確認することが可能なゲームである。また，Mastermindはゲーム事態の設定によってその基本問題空間を広げることも可能であり，難易度の実験的操作が容易である。このような理由からMastermindは，状況適応的な問題解決過程に関する認知的要因や領域知識を利用した推論などを検討するうえで適切な実験課題であるといえるであろう。 引用文献 1)田中哲郎:数当てゲーム，松原 仁・竹内郁雄編:ゲームプログラミング，150-157，共立出版，1997 2)大塚 一徳・奥田 富蔵：ワーキングメモリへの記憶負荷が問題解決に及ぼす影響,東海大学短期大学紀要,29,115-120,1995 3)奥田富蔵・大塚一徳・井上　靖:数当てゲームITSのためのプレー知識の構造について ＣＡＩ学会誌,11,183-194,1995 4)Anzai,Y.,& Simon,H.A.: The theory of learning by doing. Psychological Review,86,124-140,1979 5)Gick,M.L., & Holyoak, K.J.: Analogical problem solving. Cognitive Psychology,12,306-355,1980 6)米川　勉: 継時的に集積する情報の処理過程−記憶と処理におこるトレード・オフの軽減に関して−　心理学研究，62，96-101,1991 7)Bruner,J.S.,Goodnow,J.J., & Austin, G.A.：Astudy of thinking, New York: John Wiley & Sons,Inc.　1956,岸本弘・岸本紀子・杉崎恵義・山北　亮：思考の研究,　明治図書,1969 8)Laughlin，P．A．，Lange，R．， & Adamopoulos，J．: Selection strategies for "Mastermind" problems． Journal of Experimental Psychology: Learning，Memory， and Cognition，8，475-483，1982 9)大塚 一徳・奥田 富蔵：問題解決における言語的作動記憶容量と解決方略,東海大学短期大学紀要,31,37-42,1997 10)大塚 一徳・奥田 富蔵：問題解決における言語的作動記憶容量の制約と外的資源の利用,東海大学短期大学紀要,32,31-35,1998